Пирамида е геометриско тело кое има основа која е многуаголник и бочни ѕидови со бројност која е еднаква со бројот на страните на многуаголникот при основата.
Од една страна сите бочни ѕидови се прилепени на основата, додека од спротивната страна (ако пирамидата е цела) сите завршуваат во една иста точка, што се нарекува врв на пирамидата. Отсечката која го поврзува врвот на пирамидата со основата под прав агол, се вика висина на пирамида и се означува со H (латиница).
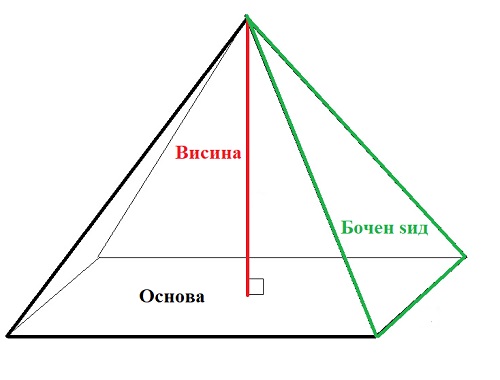
Видови пирамиди
Пирамидите може да се делат на различни видови пирамида според два различни критериуми:
a) Според геометриската форма на основата пирамидите се делат на:
- Триаголна пирамида (ако основата на пирамидата е триаголник)
- Четириаголна пирамида (ако основата на пирамидата е четириаголник)
- Петаголна пирамида (ако основата на пирамидата е петаголник)
Логично, следува дека во зависност од бројот на аглите (страните) на многуаголникот при основата, исто така се нарекува и пирамидата!
б) Според големината на аголот кој го образуваат висината на пирамидата и рамнината во која лежи нејзината основа, пирамидата може да биде:
- Рамна – ако висината и основата зафаќаат прав агол меѓусебе.
- Коса – ако висината и основата зафаќаат агол кој е различен од правиот агол.
За една пирамида може да се рече дека е правилна ако основата и е многуаголник со еднакви страни, а аголот меѓу основата и висината е прав агол. Кај овој тип на пирамиди сите бочни ѕидови се рамнокраки триаголници кои се еднакви меѓусебе.
Плоштина на пирамида
Плоштина на пирамида се пресметува со формулата:
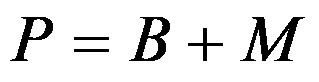
каде со B се означува плоштината на основата, додека со M се означува вкупната плоштина на бочните ѕидови.
Формулата за пресметување на плоштината на пирамида мора да се прилагоди на самиот тип на пирамидата. Ако пирамидата е триаголна, тогаш за да пресметаме плоштина на пирамидата треба да користиме формула за плоштина на триаголник, имајќи на ум дека основата е само еден триаголник, додека M е образуван од три бочни страни во форма на триаголник.
Ако пирамидата е коса, тогаш пресметката станува навистина сложена затоа што сите бочни ѕидови се различни меѓусебе.
Задача со плоштина
Пример број 1: Пресметај ја плоштината на правилна пирамида која има основа квадрат со страна 20cm, ако должината на нејзиниот бочен раб изнесува 30cm.
Постапката за решавање на задачата тече по следниот тек:
a) Пресметување на плоштината на основата по формулата за плоштина на квадрат. (вредност M)
б) Пресметување на плоштината на рамнокрак триаголник (може на повеќе начини) со херонова формула. Вредноста се множи по 4 бидејќи има четири еднакви бочни страни. (вредност B).
в) Пресметување на збир од вредноста добиена за M и вредноста добиена за B.
Решение:
а) Пресметка за плоштината на основата на пирамидата:
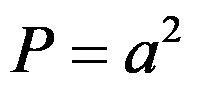
со замена на вредноста на должината на страната на основат се добива:
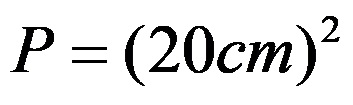
од каде што следи дека плоштината на основата изнесува 400 центиметри квадратни. Оваа вредност ја претставува вредноста B од формулата за пресметување на плоштината на пирамидата.
б) Користејќи ја хероновата формула (кликни тука за да видиш пресметка со херонова формула) за бочниот ѕид на пирамидата кој е триаголник со страни 20cm, 30cm и 30cm, за еден триаголник се добива дека има плоштина која изнесува 283 (приближно) центиметри квадратни. За да се добие целата вредност M од формулата, вредноста за плоштината на еден бочен ѕид се множи со 4, при што за вредноста на М се добива 1132 центиметри квадратни.
в) Плоштината на пирамидата се преметува како збир на B и M. при што се добива конечниот резултат 1532 центиметри квадратни.
Волумен на пирамида
Волумен на пирамида се пресметува со формулата:
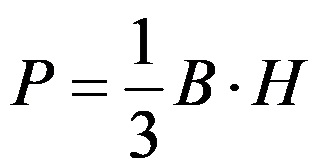
За да одредиме волумен на било која пирамида треба да пресметаме една третина од производот на плоштината на основата на пирамидата и висината на пирамидата.
Пример број 2: Пресметај го волуменот на пирамида со основа квадрат со страна 15cm, ако висината на пирамидата изнесува 25cm.
За да се реши задачата потребно е:
a) Да се пресмета плоштина на основата (по формулата за квадрат се добива 225 центиметри квадратни, (види пр. број 1).
б) Вредноста за плоштината на основата се множи со висината H. Производот на овие две вредности изнесува 5625 центиметри кубни.
в) На крај се пресметува третина од вредност добиена под б). Една третина од 5625 изнесува 1875.
Волуменот на пирамидата од примерот број 2 изнесува 1875 центиметри кубни.
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.


 Ве молиме почекајте ...
Ве молиме почекајте ...

