Лост е секое тврдо тело кое може да ротира околу некоја точка или оска, под дејство на најмалку две сили кои се стремат да предизвикаат спротивни свртувања. Лост е проста машина која се користи за на згоден начин да се користи сила со која би можеле да совладаме поголем отпор одколку без него.
За сите почетници кои изучуваат физика простите машини се првиот посериозен практичен момент кој потврдува колку самата наука ни ја олеснува работата!
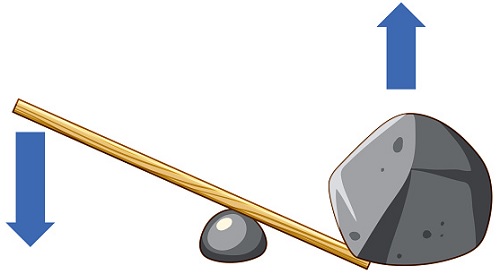
Видови лостови
Лостовите се делат според два критериуми:
а) Според поставеноста на потпорната точка или оска:
- Едностран – лост кај кој потпорната точка или оска се наоѓа не еден од неговите краеви.
- Двостран – лост кај кој потпорната точка или оска се наоѓа помеѓу двете негови крајни точки.

б) Според должината на краците (важи за двостаните лостови):
- Рамностран (рамнокрак) – лост на кој краците му се со еднаква должина.
- Разностран – лост на кој краците му се со различна должина.
Услов за рамнотежа на лост
Да претпоставиме дека на располагање имаме двостран лост. Да замислиме дека на еден од неговите краци има поставено товар, а ние дејствуваме од спротивната страна со одредена сила. Во тој случај растојанието од товарот до потпорната точка го нарекуваме крак на товар и го бележиме со b, а растојанието од местото каде што дејствува силата до потпорната точка го нарекуваме крак на сила и го означуваме со a. Сила означуваме со F, а товар со G.
Условот за рамнотежа на лост гласи:
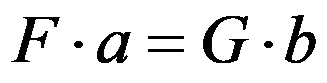
Производот F по a се нарекува момент на сила, додека производот G по b се нарекува момент на товар. Условот за рамнотежа на лост некогаш се разгледува и како урамнотежување на моменти.
Од тука, ако сакаме да ја изразиме само големината на силата, тогаш равенката по трансформацијата ја добива следната варијанта:
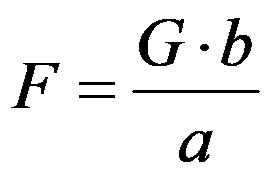
Со помош на последната формула лесно може да се пресмета колкава сила ни е потребна за да совладаме определен отпор (во форма на товар) ако ја знаеме неговата поставеност во однос на лостот, како и перформансите на самата проста машина.
Задача од лост
Пример број 1: Пресметај колкава сила е потребана за да се урамнотежи лостот на кој од една страна има поставено товар од 10000 N (њутни) на растојание од 50 центиметри од потпорната точка, ако со сила мора да се дејствува на 4 метри од спротивната страна страна во однос на потпорната точка.
Дадените податоци се:
- a=4m
- b=50cm=0,5m (потребно претворање од центиметри во метри)
- G=10000N
- F-?
Со замена на соодветните вредности во последната изведена равенка се добива следниот израз:
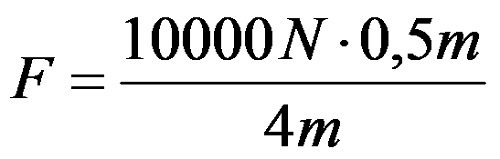
По комплетирањето на пресметката се добива дека силата изнесува 1250 њутни.
Од самата пресметка во задачата јасно се забележува корисниот ефект на лостот. Со неговата употреба може да се совлада товар од 10000 њутни, само со сила од 1250 њутни (8 пати помала сила, затоа што кракот на силата е 8 пати подолг од кракот на товарот).
Интересен факт кој покажува дека кај лостот е важна должината на кракот на силата: Архимед рекол: Дајте ми доволно долг лост и ќе ја поместам планетата Земја.
Следете ги информациите и материјалите кои ќе бидат објавени во иднина со поврзување на профилите на www.matematikazasite.com профилите на Facebook, Instagram, Twitter и Youtube со користење на копчињата подолу.
Tags: Двостран, Едностран, Крак на сила, Крак на товар, Лост, Момент на сила, Момент на товар, Рамнотежа на лост, Сила, Товар, Формула


 Ве молиме почекајте ...
Ве молиме почекајте ...

